Kamada-Kawaiのアルゴリズム
グラフが与えられたときに、それを綺麗に描画するアルゴリズムをグラフ描画アルゴリズムといいます。今回はグラフ描画アルゴリズムの一つである、Kamada-Kawaiのアルゴリズムについて説明したいと思います。
Kamada-Kawaiのアルゴリズムは、辺の重みを理想的な2点間のユークリッド距離としてエネルギー関数 $E$ を定義し、それを最小にするような節点の座標 $p_i = (x_i,y_i)^T\ (i=1,\cdots,n)$ を求めることで、綺麗なグラフを描画します。
まず、 $d_{i,j}$ を2点間の最短経路長とします。この $d_{i,j}$ を求めるアルゴリズムとして、例えばFloyd-Warshall法などがあります。次に$d_{i,j}$を用いて2点間の理想的なバネの長さ $l_{i,j}$ を定義します。
$$ l_{i,j} = Ld_{i,j} $$
$ L $は次式で計算されます。
$$ L = \max_{ i < j } \frac{ L_0 }{ d_{i,j} } $$
$L_0$は表示する画面の1辺の長さです。
また、バネの強さを次式で定義します。( $K$ は定数 )
$$ k_{i,j} = \frac{K}{d_{i,j}} $$
エネルギー関数の最小化
これで各値が求まったので、エネルギー関数 $E$ を定義し、各点の座標 $p_i=(x_i,y_i)^T $ を求めていきます。
エネルギー関数 $E$ を次式で定義します。
$$ \begin{aligned} E & \equiv \sum_{i=1}^{n-1}\sum_{j=i+1}^{n} \frac{1}{2}k_{i,j} \left( \|p_i-p_j\|-l_{i,j} \right)^2 \\ & = \sum_{i=1}^{n-1}\sum_{j=i+1}^{n} \frac{1}{2}k_{i,j} \left( (x_i-x_j)^2+(y_i-y_j)^2+l_{i,j}^2-2l_{i,j}\sqrt{(x_i-x_j)^2+(y_i-y_j)^2} \right) \end{aligned} $$
これを $p_i = (x_i,y_i)^T$ について最小にする手法はいくつかありますが、参考pdfと同じように、Newton-Raphson法で最小化したいと思います。
Newton-Raphson法では目的関数の1,2階導関数が必要なので、実際に計算をしていきます。まずは1階導関数です。
$$ \begin{aligned} \frac{\partial E}{\partial x_m} & = \sum_{i=1}^{n-1}\sum_{j=i+1}^{n} \frac{1}{2}k_{i,j} \left( \frac{\partial}{\partial x_m}(x_i-x_j)^2-2l_{i,j}\frac{\partial}{\partial x_m}\sqrt{(x_i-x_j)^2+(y_i-y_j)^2} \right) \\ & = \sum_{ i=1 }^{ m - 1 } \frac{1}{2} k_{i,j} \left( -2(x_i-x_m)-2 l_{i,m} \frac{ -( x_i - x_m ) }{ \sqrt{ (x_i - x_m )^2+( y_i - y_m )^2 } } \right) \\ & \quad +\sum_{j=m+1}^{n} \frac{1}{2}k_{i,j} \left( 2(x_m-x_j)-2l_{m,j}\frac{(x_m-x_j)}{\sqrt{(x_m-x_j)^2+(y_m-y_j)^2}} \right) \\ & = \sum_{i=1,i \neq m}^n k_{m,i}(x_m-x_i)\left( 1 - \frac{l_{m,i}}{\| p_m - p_i \|} \right) \end{aligned} $$
同様にして、$\frac{\partial E}{\partial y_m}$は、
$$ \frac{\partial E}{\partial y_m} = \sum_{i=1,i \neq m}^n k_{m,i}(y_m-y_i)\left( 1 - \frac{l_{m,i}}{\| p_m - p_i \|} \right) $$
となります。2階導関数は次式のようになります。
$$ \begin{aligned} \frac{\partial^2 E}{\partial x_m\partial y_m} & = \sum_{i=1,i \neq m}^n k_{m,i} \left(- l_{m,i} \frac{ 2( x_m - x_i )( y_m - y_i ) }{\| p_m - p_i \|^3}\times \left(-\frac{1}{2}\right) \right) \\ & = \sum_{i=1,i \neq m}^n k_{m,i}l_{m,i}\left( \frac{( x_m - x_i )( y_m - y_i )}{\| p_m - p_i \|^3 } \right) \\ \\ \frac{\partial^2 E}{\partial x_m^2} & = \sum_{i=1,i \neq m}^n k_{m,i} \left( 1 - l_{m,i} \frac{ \| p_m - p_i \| - \frac{ ( x_m - x_i )^2 }{ \| p_m - p_i \| } }{\| p_m - p_i \|^2} \right) \\ & = \sum_{i=1,i \neq m}^n k_{m,i}\left( 1 - \frac{ l_{m,i}( y_m - y_i )^2}{\| p_m - p_i \|^3 } \right) \\ \\ \frac{\partial^2 E}{\partial y_m^2} & = \sum_{i=1,i \neq m}^n k_{m,i} \left( 1- \frac{l_{m,i}(x_m-x_i)^2 }{\| p_m - p_i \|^3} \right) \end{aligned} $$
これで必要な式が求まりました。Newton-Raphson法では以下の式を繰り返し計算して近似的に極小値を求めます。 $$ \begin{aligned} H\Delta p_m & = - \nabla E \\ p_m & \leftarrow p_m + \Delta p_m \end{aligned} $$ ただし、$H$はヘッシアンといい、2変数関数の場合
$$ H = \left( \begin{array}{cc} \frac{\partial^2 E}{\partial x_m^2} & \frac{\partial^2 E}{\partial x_m\partial y_m} \\ \frac{\partial^2 E}{\partial y_m\partial x_m} & \frac{\partial^2 E}{\partial y_m^2} \end{array} \right) $$
で定義されます。 この反復計算によって求まった各節点の座標を用いることで、元々の各エッジの重みを考慮したグラフを描画することが出来ます。このとき、反復計算における終了条件として、次の値を使用します。 $$ \Delta_i = \sqrt{\left( \frac{\partial E}{\partial x_m} \right)^2 + \left( \frac{\partial E}{\partial y_m} \right)^2} $$ 擬似コードは次のようになります。- Floyd-Warshall法で$d_{i,j}$を求める
- $l_{i,j}$を求める
- $k_{i,j}$を求める
- $p_i = (x_i,y_i)^T$をランダムに初期化する
- $\mathrm{while}(\max_{i} {\Delta_i} > \varepsilon)$
- $m \leftarrow $ $\Delta_i$を最大化する$i$
- $\mathrm{while}(\Delta_m > \varepsilon)$
- $ H\Delta p_m = - \nabla E $ から$ \Delta p_m $を求める
- $ p_m \leftarrow p_m + \Delta p_m $ で座標を更新する
プログラム例
今回はC++で実装しました。実行結果
下のような無向グラフに対してプログラムを実行させました。結果はgnuplotで表示しています。5 10 0 1 1 0 2 1 0 3 1 0 4 1 1 2 1 1 3 1 1 4 1 2 3 1 2 4 1 3 4 1ただし、このデータは最初の1行が 節点数$n$、辺の本数$ m $を表し、以降の$ m $行が始点$ a_i $ 終点$ b_i $ 重み $ c_i $を表しています。このプログラムでは、コマンドライン引数で無向グラフか有向グラフかを指定できるようになっています。
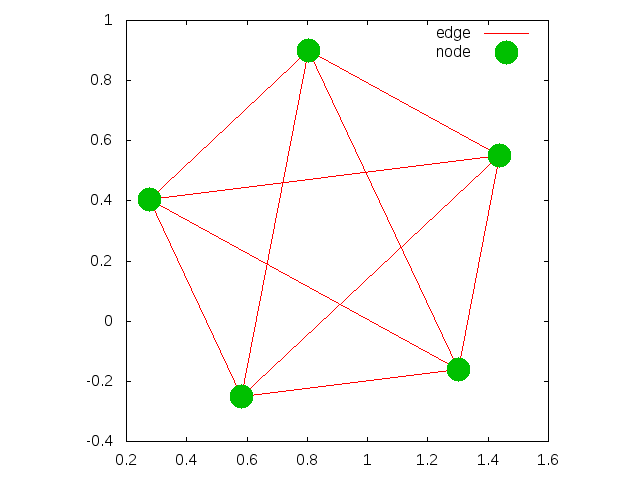
今回は$L_0=1,K=10$としました。結果を見ると、各辺の重みを考慮したグラフが描画できていることがわかります。